Utilizzo della curva di coppia e potenza del mandrino per la scelta dei parametri di taglio
PREREQUISITI
- Conoscenza base di CNC
- Conoscenza base dei processi di fresatura
- Conoscenza base di software CAD/CAM
- TEMPO DI APPRENDIMENTO: 40 min.
OBIETTIVI
- Scegliere il diametro utensile e la velocità di rotazione adeguata alla lavorazione considerando la coppia e la potenza erogabili dal mandrino
- Eseguire i calcoli utili per definire i parametri di taglio in funzione della posizione scelta nella curva caratteristica del mandrino
DOMANDE ANTICIPATIVE
Sai che la macchina potrebbe non riuscire a lavorare se non scegli correttamente i parametri di taglio considerando la coppia e la potenza erogabili dal mandrino?
Sai che non basta che il tool holder della macchina possa montare un certo diametro di utensile per essere certi che la macchina potrà sopportare le coppie e potenze che si generano in lavorazione?
Sai che i centri di lavoro sono progettati appositamente per lavorare in condizioni specifiche? In altre parole, una macchina adatta alle lavorazioni di precisione non è adatta alle lavorazioni standard
Sai calcolare le forze, le coppie e le potenze che si generano in lavorazione? È utile per scegliere gli utensili!
Scelta dellA velocità di taglio
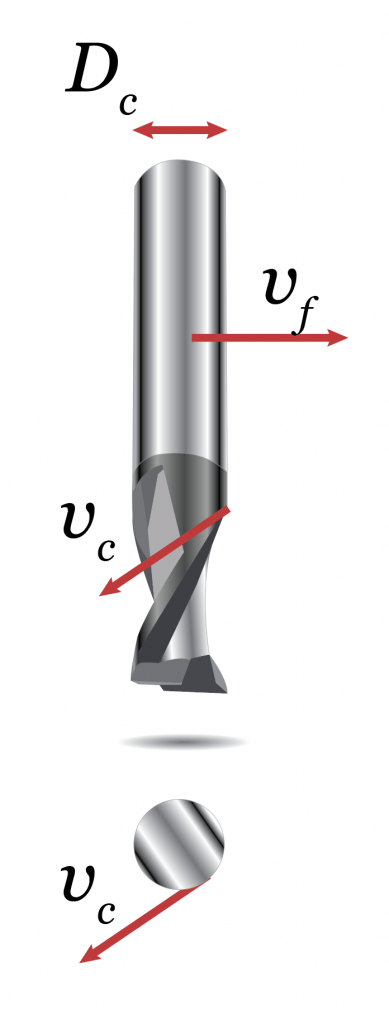
Rappresentazione delle velocità caratteristiche di un processo di fresatura.
- Dc dipende dalla geometria del pezzo da lavorare (v. “Selezione dei parametri di taglio nelle aree critiche del percorso utensile (raccordi)”).
- vc è consigliata dai produttori degli utensili in funzione della coppia materiale target – materiale dell’utensile quindi può essere considerata costante.
- Dc dipende dalla geometria del pezzo da lavorare (v. “Selezione dei parametri di taglio nelle aree critiche del percorso utensile (raccordi)”).
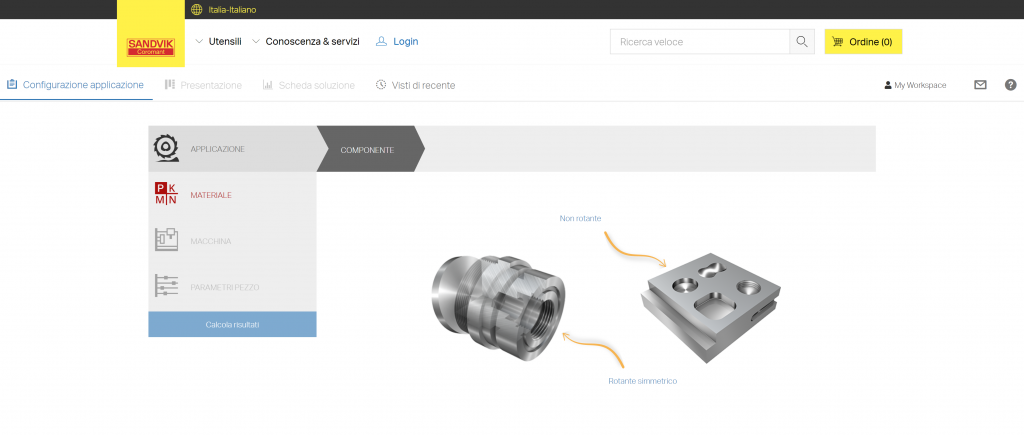
Interfaccia di CoroPlus Tool Guide, software online per la scelta dei parametri di taglio (Sandvik Coromat).
SCELTA DEL DIAMETRO DELL'UTENSILE
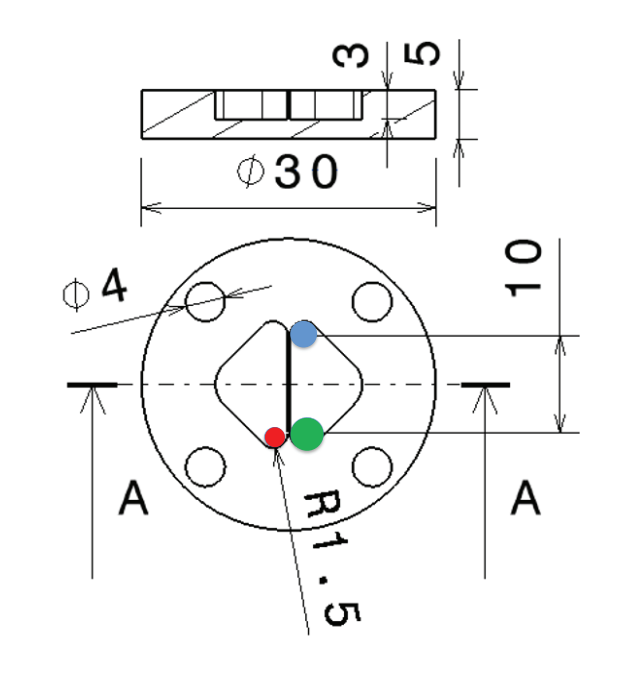
Esempio di tasche con spigoli raccordati a 1.5 mm.
Possibili diametri dell’utensile:
- Dc1 = 2 mm
- Dc2 = 2.8 mm
- Dc3 = 4 mm
La terza fresa è chiaramente non adatta, ma potremmo sceglierne una delle altre due. Dc dipende dalla geometria da realizzare. In generale, è meglio usare utensili relativamente grandi in quanto sono più rigidi, ma i raccordi nel pezzo limitano il raggio utensile (v. “Come selezionare un utensile usando un catalogo online”).
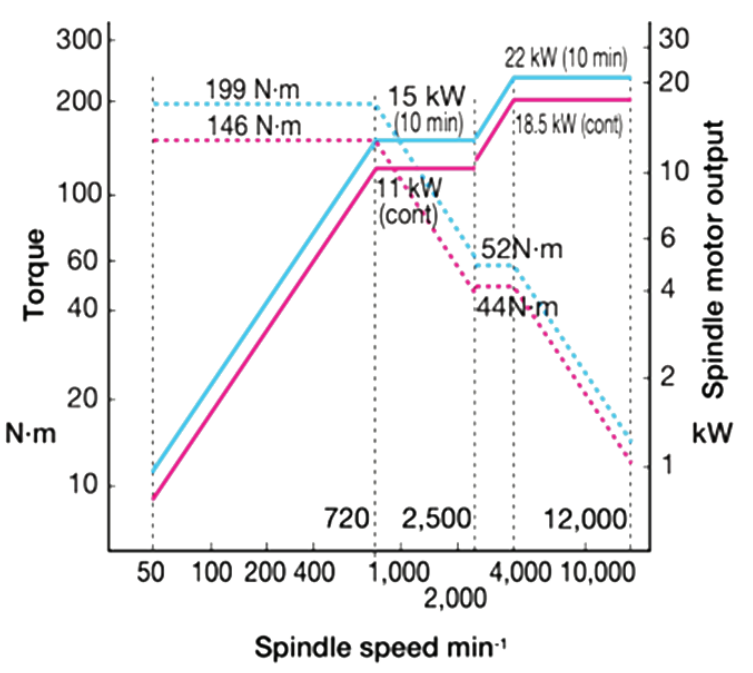
USO DEL DIAGRAMMA DI COPPIA E POTENZA DEL MANDRINO PER LA SCELTA DEI PARAMETRI
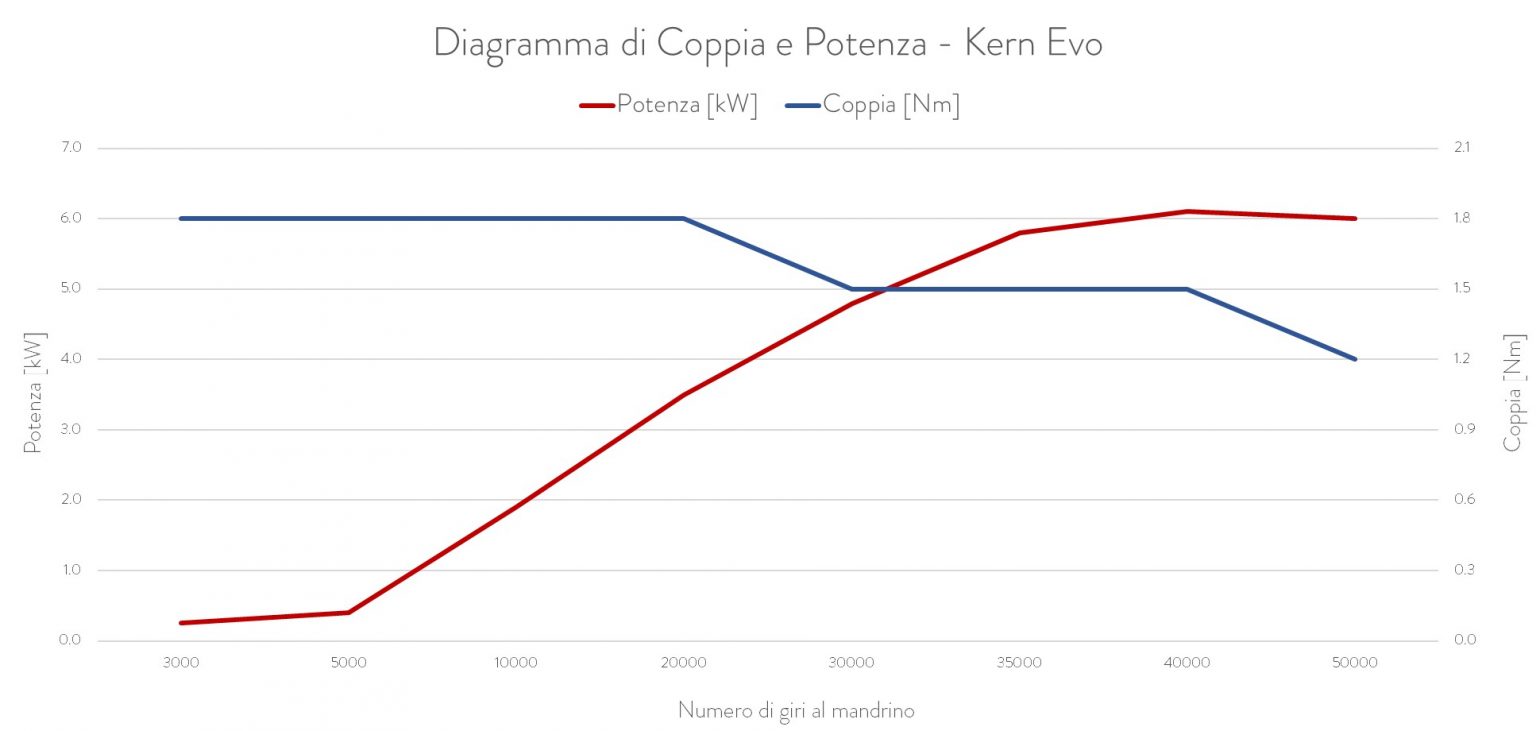

Centro di lavoro Kern Evo.
Questo diagramma è la curva caratteristica del mandrino, che ha una importanza fondamentale per scegliere l’utensile e i parametri di processo. La prima cosa da notare è che la performance di coppia e di potenza dichiarata nel datasheet della macchina si riferisce a un certo intervallo di numero di giri.
Infatti, si può vedere come la potenza massima sia fornita soltanto oltre i 40.000 giri al minuto.
Ciò significa che il mandrino della macchina è adatto a girare velocemente.
INTERAZIONE TRA DIAMETRO DELL'UTENSILE E VELOCITÀ DI TAGLIO
v_c=\frac{\pi \cdot D_\mathrm{c} \cdot n}{1000}
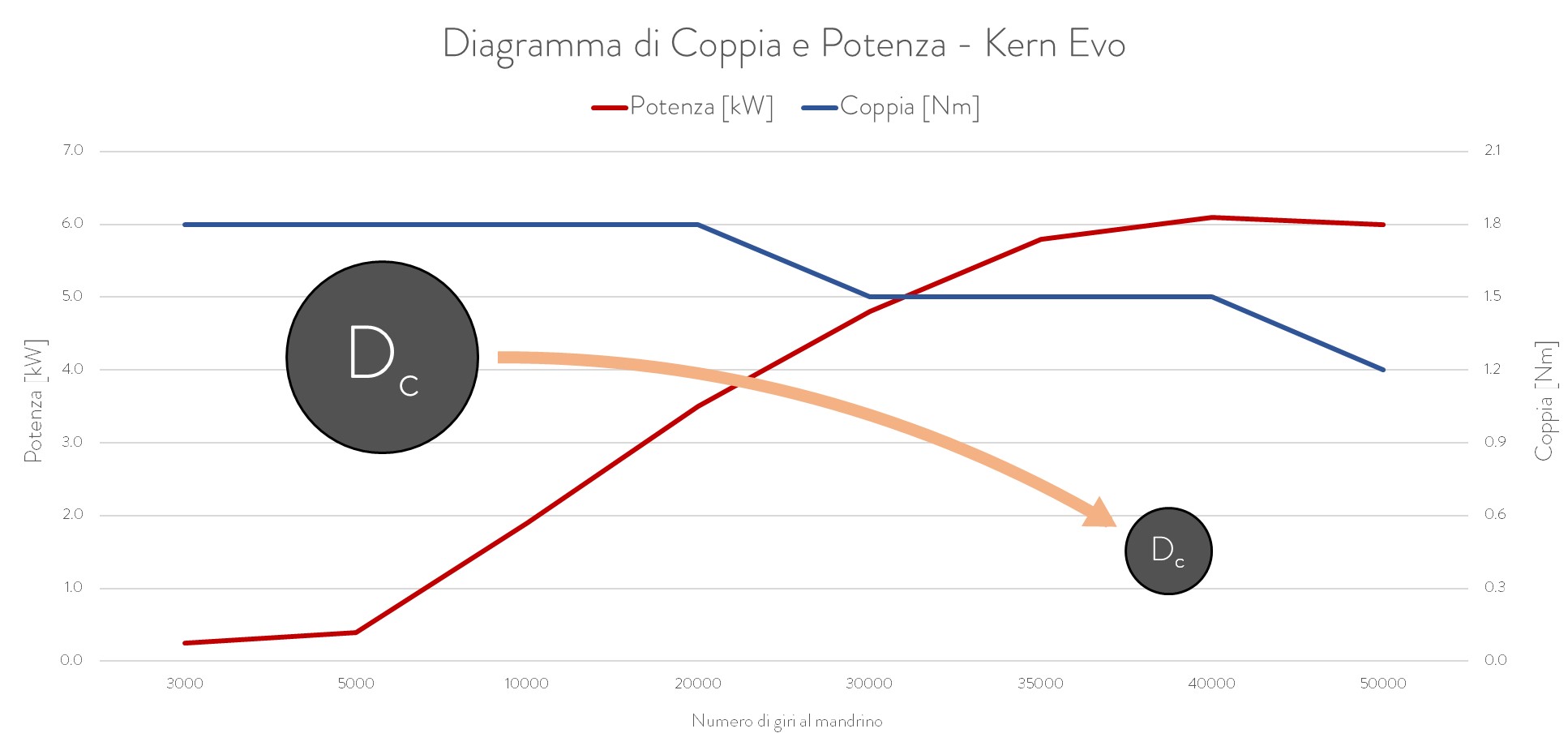
Variazione del punto di utilizzo della macchina in funzione del diametro di taglio.
VELOCITÀ DI AVANZAMENTO E TASSO DI RIMOZIONE DI MATERIALE (MICROFRESATURA)
v_\mathrm{f} = n\cdot f_\mathrm{z}\cdot Z
Z vale tipicamente 2 in microfresatura e n tende ad essere elevato per sfruttare meglio il mandrino, inoltre fz non può essere troppo piccolo per evitare il ricalcamento (minimum chip thickness effect).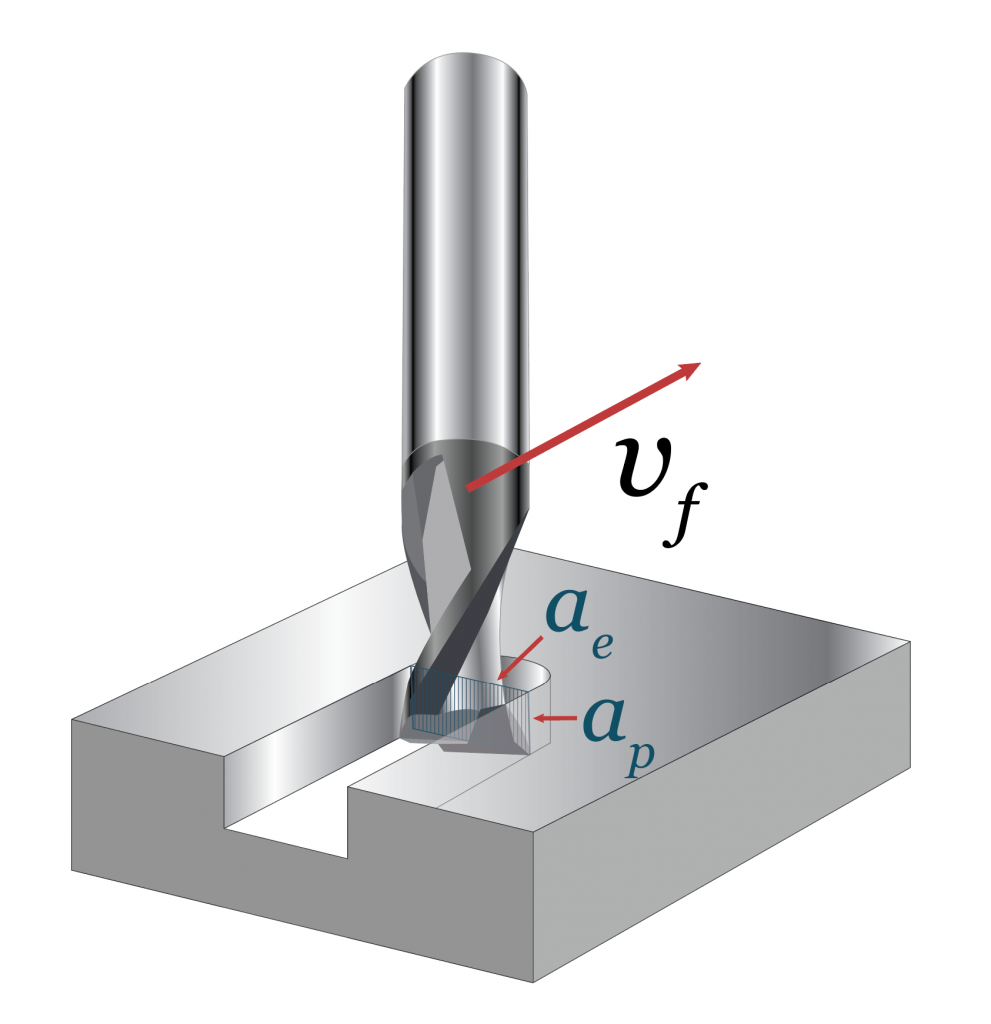
Profondità di passate assiale ap, radiale ae e velocità di avanzamento vf.
La velocità di avanzamento aumenta: questo significa che vf tende ad essere elevato in microfresatura. Per questa ragione, i centri di microfresatura devono avere una buona performance in termini di massima velocità di avanzamento.
MRR = v_\mathrm{f}\cdot a_\mathrm{p} \cdot a_\mathrm{e}
Il Material Removal Rate (MRR), o Volume di truciolo asportato (Q) è limitato da ap e ae che sono piccoli in quanto legati alle dimensioni dell’utensile.
Per massimizzare l’MRR, abbiamo già vf, ma anche la profondità di taglio deve essere considerata. ae è limitata per preservare l’integrità dell’utensile (v. “Selezione dei parametri di taglio nelle aree critiche del percorso utensile (raccordi)“). ap invece può essere aumentata secondo le indicazioni dell’utensiliere e le nuove strategie di fresatura trocoidali (bassa ae e alta ap), che sono state inventate per la fresatura ad alta velocità e la microfresatura.
FRESATURA STANDARD
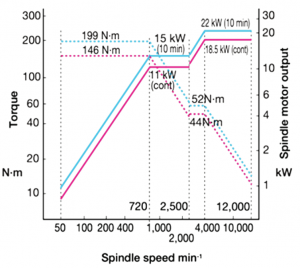

Diagramma caratteristico dell’Okuma Genos M460V.
In questo nugget, consideriamo quello che accade nelle traiettorie rettilinee. Considereremo quanto accade nelle curve nel prossimo nugget. ae gioca un ruolo sullo spessore massimo del truciolo hex tramite l’angolo di impegno della fresa. hex può essere usato per calcolare la forza di taglio massima secondo il metodo della pressione di taglio. L’angolo di spoglia frontale (ɣ0) gioca un ruolo importante nella pressione di taglio.
Come noto, quando ɣ0 aumenta, l’azione di taglio richiede una forza minore. In qualche caso, un valore rappresentativo medio della forza di taglio deve essere calcolato per un certo angolo di impegno della fresa. Lo spessore di truciolo medio hm può essere calcolato come indicato di seguito. hm può essere usato per calcolare la corrispondente pressione di taglio e forza di taglio.
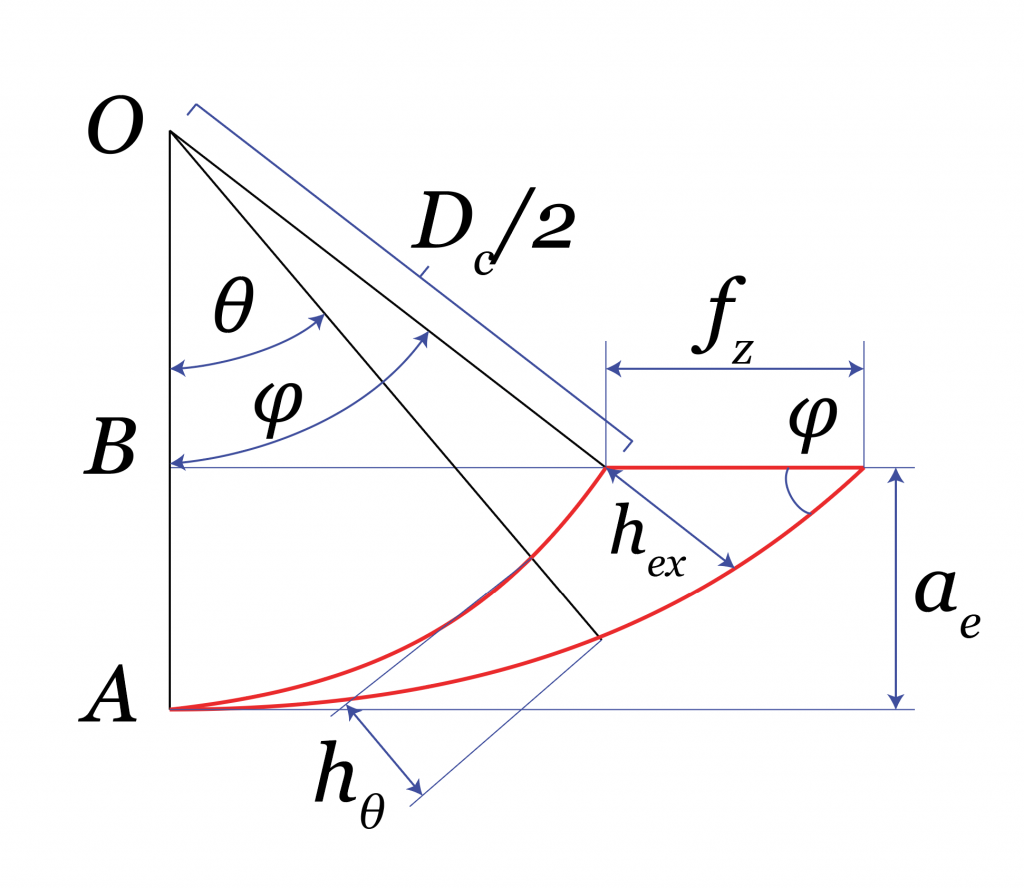
Schema per il calcolo dello spessore di truciolo medio e massimo.
Angolo di impegno della fresa:
cos(\varphi) = \frac{\frac{D_\mathrm{{c}}}{2}-a_\mathrm{e}}{\frac{D_\mathrm{{c}}}{2} } = \frac{D_\mathrm{{c}}-2a_\mathrm{e}}{D_\mathrm{{c}}} = 1 – \frac{2a_\mathrm{e}}{D_\mathrm{c}}
Approccio allo spessore di truciolo massimo:
h_\mathrm{{ex}} = f_z sin(\varphi)
k_\mathrm{{c,ex}} = k_\mathrm{{c1}}h_\mathrm{{ex}}^{-x}(1-\frac{\gamma_0}{100})
F_\mathrm{{c,ex}} = k_\mathrm{{c,ex}}A_\mathrm{D} = k_\mathrm{{c,ex}}h_\mathrm{{ex}}a_\mathrm{p}
Approccio allo spessore di truciolo medio:
h_\mathrm{m}=\frac{2f_\mathrm{z}a_\mathrm{e}}{\varphi D_\mathrm{{c}}}
k_\mathrm{{c,m}} = k_\mathrm{{c1}}h_\mathrm{{m}}^{-x}(1-\frac{\gamma_0}{100})
F_\mathrm{{c,m}} = k_\mathrm{{c,m}}A_\mathrm{D} = k_\mathrm{{c,m}}h_\mathrm{m}a_\mathrm{p}
kc1: Pressione di taglio di riferimento (N/mm2)
x: Coefficiente del materiale dell’utensile (ad es. x = 0,25)
kre = 90° (fresa a candela)
Note:
- Esprimere ɣ0 in valori decimali nella formula di kc,ex
- In generale usiamo lo spessore medio di truciolo per calcolare la forza valido anche per valori di φ > 90°, anche se in quel caso sottostimerebbe il valore dello spessore massimo del truciolo. Nel nostro caso, abbiamo φ < 90°, così possiamo usare hex espresso dalla formula indicata per essere conservativi. In questo modo, possiamo calcolare lo spessore massimo di truciolo e la forza massima.
COPPIA DI TAGLIO, POTENZA E DEFLESSIONE UTENSILE
Considerando che solo un tagliente è impegnato alla volta, possiamo usare semplici formule per calcolare la coppia e la potenza di taglio. Come fatto precedentemente, ci riferiamo allo spessore di truciolo medio e allo spessore di truciolo massimo hm e hex.
M_\mathrm{{c,m}} = F_\mathrm{{c,m}}\frac{D_\mathrm{c}}{2}
M_\mathrm{{c,ex}} = F_\mathrm{{c,ex}}\frac{D_\mathrm{c}}{2}
P_\mathrm{c} = F_\mathrm{c}v_\mathrm{c}*
Momento di inerzia di una sezione circolare (modelliamo la fresa come un cilindro; in questo modo sovrastimiamo J):
J = \frac{\pi D_\mathrm{c}^4}{64}
La deflessione utensile che viene espressa nella seguente equazione gioca un ruolo sull’accuratezza del pezzo.
d = \frac{F_\mathrm{c}L^3}{3EJ}**
*Formula valida per un tagliente impegnato
**L è la lunghezza a sbalzo (consideriamo la fresa come una trave incastrata)
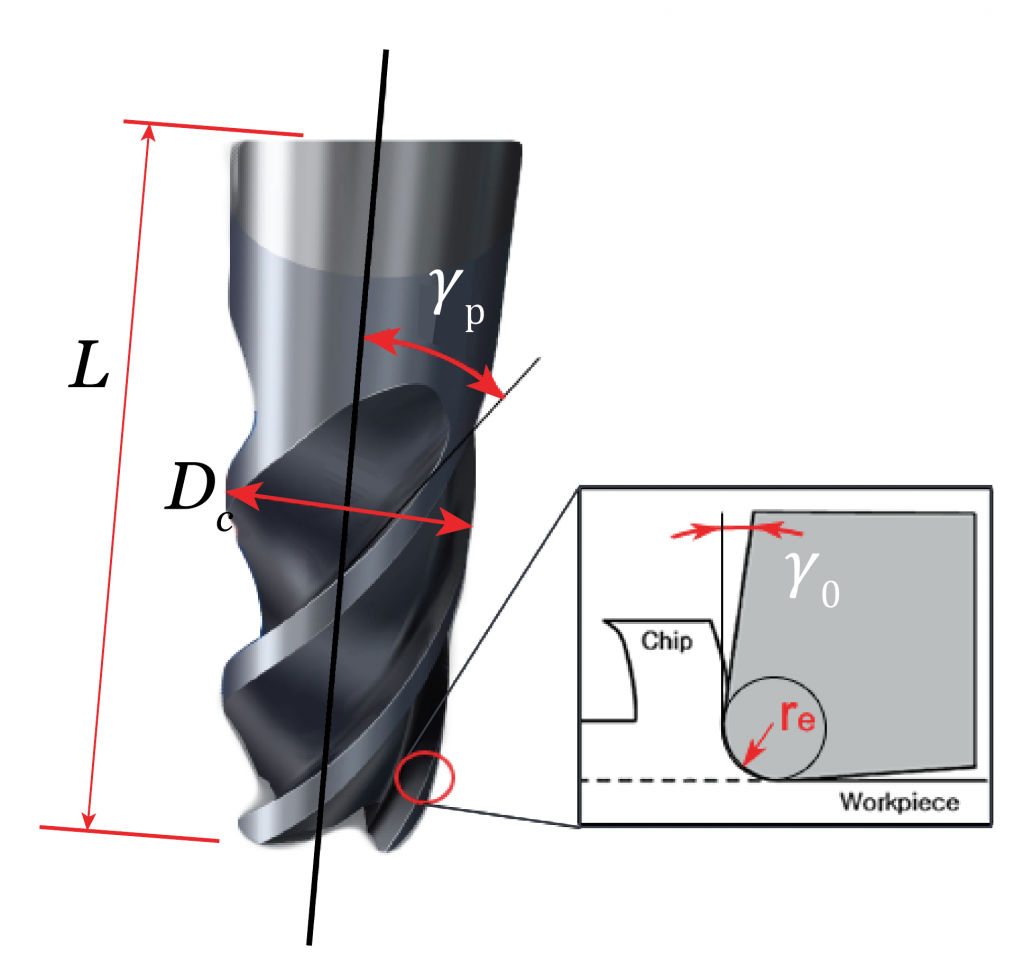
Schema delle grandezze caratteristiche di una fresa: diametro di taglio Dc, lunghezza a sbalzo L, angolo d’elica ɣp, angolo di spoglia frontale ɣ0 e raggio di punta dello spigolo re.
- COMPETENZE ACQUISITE
Hai acquisito le seguenti competenze:
- Scegliere i parametri di taglio tenendo conto della curva di coppia e potenza del mandrino della macchina.

CONTATTI UTILI, LINK E DOWNLOAD
Contatti
- Per gli studenti:
Prof. Massimiliano Annoni, Politecnico di Milano: massimiliano.annoni@polimi.it - Per gli educatori:
Prof. Massimiliano Annoni, Politecnico di Milano: massimiliano.annoni@polimi.it - Per le imprese:
Prof. Massimiliano Annoni, Politecnico di Milano: massimiliano.annoni@polimi.it
- LEARNING TIME: -- min.